Algorithm

Floyd-Warshall Algorithm:

1. Initialize a 2D array `dist[][]` to represent the shortest distances between every pair of vertices.
2. Set `dist[i][j]` to the weight of the edge between vertex `i` and vertex `j`. If no edge exists, set it to infinity (`INF`).
3. For each vertex `k` in the graph:
   1. For each pair of vertices `(i, j)`:
      1. Check if the vertex `k` can be used as an intermediate vertex to provide a shorter path from `i` to `j`.
      2. If `dist[i][k] + dist[k][j] < dist[i][j]`, update `dist[i][j]` to `dist[i][k] + dist[k][j]`.
4. After processing all vertices, `dist[i][j]` will contain the shortest distance between vertex `i` and vertex `j`.

Example:

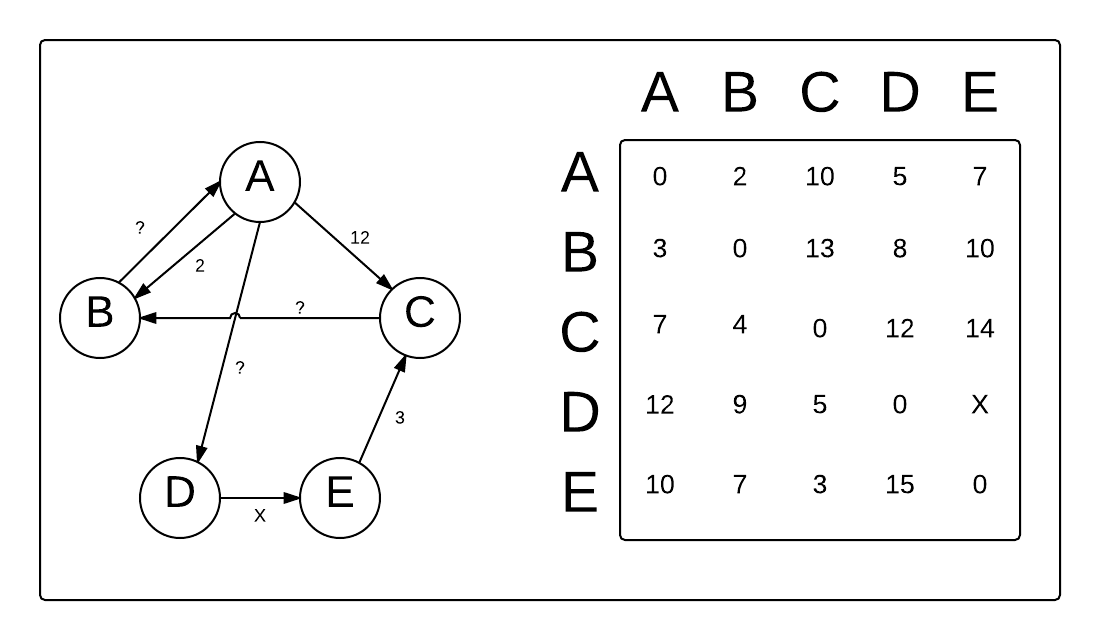
Fig. 1: Step-by-Step Process of Floyd-Warshall Algorithm

Note: The Floyd-Warshall Algorithm works for both directed and undirected graphs but does not handle negative weight cycles.